CAMINO MAS CORTO: ALGORITMO DE BELLMAN-FORD

En esta oportunidad se explicará el algoritmo de Bellman-Ford para hallar la ruta más corta, comenzaremos con una breve introducción al problema de hallar la ruta más corta sobre pesos negativos y luego continuaremos con el algoritmo de Bellman-ford.

Algoritmo de Dijkstra y Pesos Negativos

Si el grafo posee pesos negativos, el algoritmo de Dijkstra puede producir respuestas incorrectas. Por ejemplo tengamos el siguiente grafo:

Si deseo la ruta más corta partiendo desde el vértice 1 según dijkstra la ruta más corte de vértice 1 al vértice 3 sería 2. Sin embargo la ruta más corta en realidad es de 1 (1 -> 2 -> 4 ->3).

Ciclos Negativos

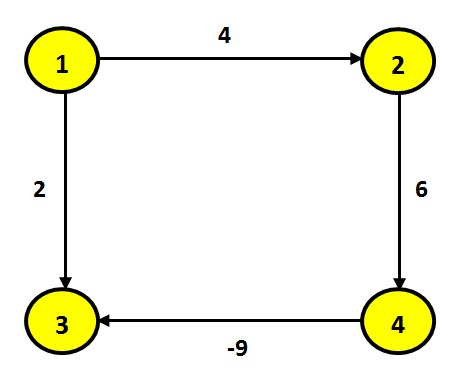
Cuando consideremos pesos negativos en las aristas, al momento de hallar la ruta más corta, es posible que se generen ciclos. Veamos el siguiente ejemplo:

Tratemos de hallar la ruta más corta aplicando Dijkstra desde el vértice 1:

Partimos de vértice 1 con peso igual a 0 y actualizamos peso de vértice 2:

Ahora actualizamos peso de vértice 3:

Según el algoritmo descrito en CAMINO MAS CORTO: ALGORITMO DE DIJKSTRA. El algoritmo terminaría, eso se da debido a que estábamos usando una arreglo de visitados de esta manera no caería en ciclos negativos; sin embargo la solución no sería correcta. Si omitimos el arreglo de visitados para hallar la ruta más corta, el algoritmo caería en un ciclo:

Como se puede ver en la figura, tenemos un ciclo negativo ya que siempre encontrará una mejor ruta entre los vértices 2 y 3.

Algoritmo de Bellman-Ford

Descripción

El algoritmo de Bellman-Ford determina la ruta más corta desde un nodo origen hacia los demás nodos para ello es requerido como entrada un grafo cuyas aristas posean pesos. La diferencia de este algoritmo con los demás es que los pesos pueden tener valores negativos ya que Bellman-Ford me permite detectar la existencia de un ciclo negativo.

Como trabaja

El algoritmo parte de un vértice origen que será ingresado, a diferencia de Dijkstra que utiliza una técnica voraz para seleccionar vértices de menor peso y actualizar sus distancias mediante el paso de relajación, Bellman-Ford simplemente relaja todas las aristas y lo hace |V| – 1 veces, siendo |V| el número de vértices del grafo.

Para la detección de ciclos negativos realizamos el paso de relajación una vez más y si se obtuvieron mejores resultados es porque existe un ciclo negativo, para verificar porque tenemos un ciclo podemos seguir relajando las veces que queramos y seguiremos obteniendo mejores resultados.

Algoritmo en pseudocódigo

Considerar distancia[ i ] como la distancia más corta del vértice origen ingresado al vértice i y |V| el número de vértices del grafo.

1  método BellmanFord(Grafo,origen):
2      inicializamos las distancias con un valor grande
3      distancia[ origen ] = 0
4      para i = 1 hasta |V| - 1:
5          para cada arista E del Grafo:
6              sea ( u , v ) vértices que unen la arista E
7              sea w el peso entre vértices ( u , v )  
8              Relajacion( u , v , w )
9      para cada arista E del Grafo:
10         sea ( u , v ) vértices que unen la arista E
11         sea w el peso entre vértices ( u , v )  
12         si Relajacion( u , v , w )
13            Imprimir “Existe ciclo negativo”    
15            Terminar Algoritmo             

1  Relajacion( actual , adyacente , peso ):
2      si distancia[ actual ] + peso < distancia[ adyacente ]
3         distancia[ adyacente ] = distancia[ actual ] + peso

Ejemplo y Código paso a paso

Tengamos el siguiente grafo, cuyos ID están en color negro encima de cada vértice, los pesos esta en color azul y la distancia inicial en cada vértice es infinito

Algunas consideraciones para entender el código que se explicara junto con el funcionamiento del algoritmo.

#define MAX 105 //maximo numero de vértices
#define Node pair< int , int > //definimos el nodo como un par( first , second ) donde first es el vertice adyacente y second el peso de la arista
#define INF 1<<30 //definimos un valor grande que represente la distancia infinita inicial, basta conque sea superior al maximo valor del peso en alguna de las aristas

Inicializamos los valores de nuestros arreglos:

Dónde:

• Vértices: ID de los vértices.
• Distancia[ u ]: Distancia más corta desde vértice inicial a vértice con ID = u.
• Previo[ u ]: Almacenara el ID del vértice anterior al vértice con ID = u, me servirá para impresión del camino más corto.

En cuanto al código los declaramos de la siguiente manera:

vector< Node > ady[ MAX ]; //lista de adyacencia
int distancia[ MAX ];      //distancia[ u ] distancia de vértice inicial a vértice con ID = u
int previo[ MAX ];         //para la impresion de caminos
int V;                     //numero de vertices

Y la función de inicialización será simplemente lo siguiente:

//función de inicialización
void init(){
    for( int i = 0 ; i <= V ; ++i ){
        distancia[ i ] = INF;  //inicializamos todas las distancias con valor infinito
        previo[ i ] = -1;      //inicializamos el previo del vértice i con -1
    }
}

De acuerdo al vértice inicial que elijamos cambiara la distancia inicial, por ejemplo la ruta más corta partiendo del vértice 1 a todos los demás vértices.

Inicialmente la distancia de vértice 1 -> vértice 1 es 0 por estar en el mismo lugar.

    distancia[ inicial ] = 0;      //Este paso es importante, inicializamos la distancia del inicial como 0

Hasta este momento la tabla quedaría de la siguiente manera:

Ahora según Bellman-Ford debemos realizar el paso de relajación |V| – 1 = 5 – 1 = 4 veces para cada arista:

    for( int i = 1 ; i <= V - 1 ; ++i ){ //Iteramos |V| - 1 veces
        …
    }

 Primera Iteración

Empezamos con las aristas que parten del vértice 1:

Como podemos observar tenemos 2 aristas, la que une vértice 1 con vértice 2 y vértice 1 con vértice 4. Ello en código:

    for( int actual = 1 ; actual <= V ; ++actual ){  //Estos dos for = O(E)
       for( int j = 0 ; j < ady[ actual ].size() ; ++j ){ //reviso sus adyacentes del vertice actual
           int adyacente = ady[ actual ][ j ].v;    //id del vertice adyacente
           int peso = ady[ actual ][ j ].w;        //peso de la arista que une actual con adyacente ( actual , adyacente )
           …
       }
    }

Las aristas de acuerdo al código serian de la forma e = (actual , adyacente , peso) donde actual es el vértice de donde partimos (en este caso sería 1) adyacente son los vértices que unen la arista e  (en este caso serían los vértices 2 y 4) y peso son los pesos de cada arista (en este caso tendríamos 7 y 2).

Evaluamos primero para vértice 2:

Vemos que la distancia actual desde el vértice inicial a 2 es ∞, verifiquemos el paso de relajación:

distancia[ 1 ] + 7 < distancia[ 2 ]    ->        0 + 7 < ∞         ->         7 < ∞

El paso de relajación es posible realizarlo entonces actualizamos la distancia en el vértice 2 quedando:

El paso de relajación se daría en la siguiente parte:

    for( int actual = 1 ; actual <= V ; ++actual ){  //Estos dos for = O(E)
       for( int j = 0 ; j < ady[ actual ].size() ; ++j ){ //reviso sus adyacentes del vertice actual
           int adyacente = ady[ actual ][ j ].v;    //id del vertice adyacente
           int peso = ady[ actual ][ j ].w;        //peso de la arista que une actual con adyacente ( actual , adyacente )
           //Realizamos paso de relajacion para la arista actual
           relajacion( actual , adyacente , peso );
       }
    }

Donde la función de relajación seria

//Paso de relajacion
void relajacion( int actual , int adyacente , int peso ){
    //Si la distancia del origen al vertice actual + peso de su arista es menor a la distancia del origen al vertice adyacente
    if( distancia[ actual ] + peso < distancia[ adyacente ] ){
        distancia[ adyacente ] = distancia[ actual ] + peso;  //relajamos el vertice actualizando la distancia
        previo[ adyacente ] = actual;                         //a su vez actualizamos el vertice previo
        Q.push( Node( adyacente , distancia[ adyacente ] ) ); //agregamos adyacente a la cola de prioridad
    }
}

Ahora evaluamos al siguiente adyacente que es el vértice 4:

De manera similar al anterior vemos que la distancia actual desde el vértice inicial a 4 es ∞, verifiquemos el paso de relajación:

distancia[ 1 ] + 2 < distancia[ 4 ]    ->        0 + 2 < ∞         ->         2 < ∞

El paso de relajación es posible realizarlo entonces actualizamos la distancia en el vértice 4 quedando:

Hemos terminado las aristas que parten del vértice 1, continuamos con las aristas que parten del vértice 2:

Comenzamos por el vértice 3 y realizamos paso de relajación:

distancia[ 2 ] + 1 < distancia[ 3 ]    ->        7 + 1 < ∞         ->         8 < ∞

En esta oportunidad hemos encontrado una ruta más corta partiendo desde el vértice inicial al vértice 3, actualizamos la distancia en el vértice 3 y actualizamos el vértice previo al actual quedando:

Ahora continuamos con la arista que une al vértice 2 con el vértice 4:

En este caso vemos que no se lleva acabo el paso de relajación:

distancia[ 2 ] + 2 < distancia[ 4 ]    ->        7 + 2 < 2         ->         9 < 2

Por lo tanto no actualizamos valores en la tabla. Ahora el siguiente vértice a evaluar es el vértice 3 que posee una sola arista:

Como el peso de su vértice adyacente es infinito actualizamos la distancia:

Ahora el siguiente vértice a evaluar es el vértice 4 que posee cuatro aristas:

Realizamos paso de relajación para cada vértice adyacente:

Con vértice 2:  distancia[ 4 ] + 3 < distancia[ 2 ]    ->     2 + 3 < 7        ->       5 < 7

Con vértice 3:  distancia[ 4 ] + 8 < distancia[ 3 ]    ->     2 + 8 < 8       ->       10 < 8

Con vértice 5:  distancia[ 4 ] + 5 < distancia[ 5 ]    ->      2 + 5 < 13     ->       7 < 13

Actualizamos distancias para los vértices 2 y 5:

Ahora continuamos con vértice 5:

En este caso no actualizamos las distancias. Hemos terminado la primera iteración, continuemos:

Segunda Iteración:

Luego de la segunda iteración obtendremos lo siguiente:

En esta iteración solamente se realizó el paso de relajación en la arista que une vértices 2 y 3. Para el grafo dado en la segunda iteración ya habremos obtenido la ruta más corta partiendo del vértice 1 a todos los demás vértices. Sin embargo no siempre obtendremos el óptimo en la 2da iteración, todo dependerá del grafo ingresado.

Impresión del Camino Más Corto

La impresión del camino más corto dado un vértice destino es de la misma forma como se explicó en el tutorial del Algoritmo de Dijkstra.

Detección de Ciclo Negativo

Para la detección de ciclo negativo tomaremos como ejemplo el grafo siguiente:

Asumimos que el vértice inicial es el vértice 1, tendremos que realizar 2 iteraciones.

Primera Iteración

Empezamos por el vértice 1:

Continuamos con el vértice 2:

Continuamos con el vértice 3:

Segunda Iteración

En esta última iteración se relajan vértices 2 y 3:

Hemos terminado el número de iteraciones que teníamos que realizar. Para verificar la existencia de un ciclo negativo, según el algoritmo de Bellman-Ford, realizamos el paso de relajación sobre todas las aristas una vez más:

Como se pudo realizar el paso de relajación entonces existe un ciclo negativo:

//Comprobamos si hay ciclo negativo en el grafo ingresado
    for( int actual = 1 ; actual <= V ; ++actual ){  //Estos dos for = O(E)
        for( int j = 0 ; j < ady[ actual ].size() ; ++j ){ //reviso sus adyacentes del vertice actual
            int adyacente = ady[ actual ][ j ].v;    //id del vertice adyacente
            int peso = ady[ actual ][ j ].w;       //peso de la arista que une actual con adyacente ( origen , destino )
            //Si aun es posible relajar la arista actual entonces tenemos ciclo negativo
            if( relajacion( actual , adyacente , peso ) ){
                puts("Existe Ciclo Negativo");
                return;
            }
        }
    }

Problemas de diferentes Jueces

UVA

117 –The Postal Worker Rings Once

558 – Wormholes

10557 – XYZZY

11280 – Flying to Fredericton

11721 – Instant View of Big Bang

LightOJ

1074 – Extended Traffic

1108 – Instant View of Big Bang

1221 – Travel Company

Códigos:

Implementación del algoritmo en C++: Algoritmo de Bellman-Ford

Por Jhosimar George Arias Figueroa